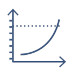
当需要较高的间歇功率密度值时,人们不希望使用传统的均方根(RMS)计算,转速-转矩性能曲线就成为了为挑选伺服电机和驱动器的唯一方法。这样做可能会导致电机或驱动器容量不足。
本文提出了一种在应用中I_actual(实际电流)长时间大于I_continuous(持续电流)时加强伺服电机热时间常数动态影响严重程度风险管理和理解的可视化方法。
伺服电机由于其内部损耗而产生热量,而且每个电机的自身散热能力决定了其额定连续容量。传统的伺服电机应用需要多种不同速率,同时要求转矩在定义的运动曲线上小于或大于电机的额定间歇转矩。传统上,通过超过伺服电机连续能力的峰值电流来实现加减速要求。运动曲线大多情况下要求这些峰值电流的持续时间段(通常在毫秒范围内)最大不超过驱动放大器一般允许的4-5秒。在这种常规间歇工作运行情况下,通常不需要根据应用的峰值转矩要求,在电机的连续能力范围内选择电机。我们只需利用均方根(RMS)方程来找到应用的有效连续转矩(Trms)和速率(Nrms)要求,然后确保此等效操作要求落在所选电机的连续和热能力范围内;同时验证在所需的转速(每分钟转数)下,所需的峰值转矩(Tpk_required)小于所选电机和驱动器提供的峰值转矩(Tpk_available)。
应用:特殊工况
将闭环运动控制技术扩展到不太传统的应用中,通常会导致超出常规间歇工作的特定要求和/或运行工况。然而,即使在传统应用中,我们有时也会遇到必须满足的特殊工况。 对于一些大型机器,急停的时间要求在20到40秒的范围内并不少见。 示例: 可能会要求一旦发生急停(紧急停止),必须在断开主电源之前在特定时间内停止所有受控运动。对于大多数应用来说,这通常不是问题,但在具有巨大动能的大型机器上,使轴运动停止所需的时间很容易超过电机驱动组合典型的最长4-5 秒的可用峰值电流 [驱动电流Ic(drive)大约等于电机电流Ic(motor)]时间。:特殊工况 将闭环运动控制技术扩展到不太传统的应用中,通常会导致超出常规间歇工作的特定要求和/或运行工况。然而,即使在传统应用中,我们有时也会遇到必须满足的特殊工况。 对于一些大型机器,急停的时间要求在20到40秒的范围内并不少见。

示例:
可能会要求一旦发生急停(紧急停止),必须在断开主电源之前在特定时间内停止所有受控运动。对于大多数应用来说,这通常不是问题,但在具有巨大动能的大型机器上,使轴运动停止所需的时间很容易超过电机驱动组合典型的最长4-5 秒的可用峰值电流 [驱动电流Ic(drive)大约等于电机电流Ic(motor)]时间。
这一要求虽然通常不需要更大的电机,但通常需要更高的连续电流驱动,以确保提供急停减速期间所需的峰值电流(Ipk_required)。对于一些大型机器,急停时间要求在20到40秒范围内并不少见。
当今的许多脉宽调制(PWM)驱动器都设计有折返过载电路或算法,利用铜线圈(TCT_coil)的热时间常数,无论电流是折回驱动器还是电机的连续电流。然而,为了满足其中一些非典型的伺服应用,一般选用的正常配对电机驱动组合并不令人满意。

当今相当多的伺服电机应用具有特殊的运行工况或面临可能发生的特殊事件,在伺服电机定规和选型过程中需要考虑这些工况或事件。
其他示例:
• 在接合静态制动器之前,伺服电机需要在特定时间内在垂直轴上承受大于其连续能力的负载(在正常生产周期中通常不希望不断接合和分离静态保持制动器)。
• 在准备应对意外事件(比如负载被卡住或运动受阻)时可能会对轴提出要求。这时电机必须能够在受令运动(但不是正常工作)的整个持续时间内承受一些峰值电流。
无论环境(例如正常大气、辐射、太空或海底、环境)是否导致易于还是无法更换电机,均应选择合适的伺服电机和驱动器组合以最大限度地降低由于特定事件或操作要求带来的故障风险,从而最大限度地提高可靠性和安全性。
过载:功率损耗的影响
根据要求的复杂性,许多应用都要求转矩和电流高于电机的持续转矩和电流(Ic 或 I_rated)作为所需RPM(例如 Npk、Nrms)的因变量。因此,需要考虑电机功率损耗的潜在限制或控制,以便完成工作或特定事件,同时保护电机的绝缘系统免受热过载的影响。此时,电机所需的电流 (I_actual) 在相对电机总热时间常数 (TCT_motor)足够长的时间内大于电机的连续额定电流 (Ic) 能力,而由于所使用的非均质材料之间的相对传热速率,TCT_motor将由TCT_coil主导。对于评估中的这些特定情况或事件,尽管仍然需要确保整体产品选择要求,[上述]引用的给定运动曲线上的RMS计算通常是无效的。过载情况可能因应用不同而差异巨大。
因此,对于这些具有某些潜在事件或其他情况的应用,需要特定的峰值电流(I_actual)才能在合格的时间段内产生特定的峰值转矩(Tpk)。此时,我们还需要了解并确定电机的绕组/线圈是否可以在不损坏电机绝缘的情况下维持所需的过载电流。
温度每超过连续额定值10°C,电机绝缘的可用寿命(基于其连续额定值)就会大约减半。
我们可以使用以下公式估算电机线圈/绕组从冷启动(环境)到额定极限温度(t_ ultimate)的时间:
t_ultimate = -TCT_coil(mounted) x ln[1-(W_loss(rated)/W_loss(actual))] or
或
t_ult. = -TCT_winding x ln[1-(Ic2/I_actual2)]
其中W_loss(rated)替换为Ic2 或I_rated2,W_loss(actual)替换为I_actual 2
技术说明:
在这些条件下,I_actual将大于电机的Ic(伺服电机在低转速或失速时的连续额定电流;在这种情况下,实际W_loss将继续上升到额定值以上,这可能会导致热失控,这取决于是否及时断开电源)。
公式假设
当然,上述用适当的I2代替分子和分母中的功率损耗特的前提是,假设在施加恒定的[阶跃输入]电流的情况下功率耗散恒定。但在实际绕组温度从环境温度(例如Rm(25°C))上升到基于W_loss(actual)的目标温度的情况下,该假设是不正确的,但提供了一种假设Rm(hot)常数求解动态非线性微分方程的方法。此外,从基于 Irms 值的非环境温度开始的实际电机应用需要进一步的干预。
但是,无论方程是被处理过,往往只需要一两个点上完成预先计算,并且实际电流(I_actual)大于连续能力(Ic)的实质性影响经常被忽略(未特别可视化)。因此,本文的目的是提供一种图形增强方法(图A)以演示需求Watts_loss大于连续能力时的影响,并以图形方式确定特定评估条件下的相对(如果无效)TCT,以克服设计挑战:I_actual(评估中)/ Ic(连续电流)大于1,并且产生应用所需的扭矩(T_required)时已知。用户还可以利用图B对特定条件下的有效TCT_motor和TCT_(air)进行相对的对比。但是,需要注意的是,在给定条件下,电机安装线圈的热时间常数(TCT_coil(mounted))相对TCT_motor占主导地位,而且TCT_coil(air)可能过于保守而无法合理使用(它是根据电磁线的比质量计算得出的,而不考虑它是否安装在电机外壳内)。 TCT_coil(mounted),以下称为TCT_winding,代表热非均匀电机材料(例如线圈与环氧树脂/空气和硅钢片)的第一级材料接触。
由于I_actual(评估中)> Ic,因此公布的TCTs [coil(air),winding(已安装线圈)和moter]不再像I_actual <= Ic时那样恒定,所考虑的热时间常数随着电机的实际功率损耗(W_loss(actual))而动态变化。例如,当实际电流(评估中)<= Ic时,给定伺服电机的公开TCT的相对范围可能为TCT_coil(air)= 25秒,TCT_winding = 60秒,TCT_motor = 600秒;然而,当I_actual > Ic时,由于W_loss(actual) 和W_loss(rated)的差异,有效TCT将比发布的TCT显著减少。
我们这个时代的大多数伺服电机在电机绕组、硅钢片和外壳之间具有良好的导热性,尤其是采用环氧树脂封装时;然而,这些仍然是非均质材料,具有显著不同的传热能力(导热性)。
过载对热时间常数(TCT)的影响
在下图 A 中,特定条件下I_actual大于 Ic(motor)的I_显著性可以通过W_loss(actual) / W_loss(rated)的百分比来表示,两者都给出了相对于计算的热时间常数 (TCT)倍数的曲线图(例如,I_actual = 5xIc 时要求绕组耗散的功率比其额定连续能力时多2500% (25x))。

下一页的图B允许我们以图形方式确定特定的TCT,从而确定所评估的特定条件下达到极限温度的时间,其方法是将图形的X轴对应(TCT)倍数作为所需I_actual相对于已知TCT的函数;然后将该结果乘以 5,以确定达到极限温度的时间。

示例:
问题1: 无论驱动器的供电能力如何,假设我们从一开始就处于25°C的环境温度,电机能否在20秒时间内承受3倍IC的峰值电流?假定最初提出的电机应用在正常运行时TCT_winding= TCT_coil(mounted)=60秒。
Q1 答: 使用图 B,我们只需转到左侧的垂直刻度 3 (3xIc) 并沿水平移动,直到与曲线相交,然后在半对数刻度上读取相应的 X 轴乘数,将其和公布的TCT_winding相乘。
3Ic 时 X对数轴的读数约为0.023,因此,在3Ic时,有效TCT_winding(3Ic) = 0.023 x 60 = ~1.38_sec。
注意: 95%的热上升将发生在3倍(热时间常数)或~4.14内[3x1.38秒],其中5xTCT或6.9秒(达到极限额定绕组温度的总时间)上升99.3%。
因此,对于此应用,我们将需要选择更大的电机或具有更长TCT_winding的电机,或更改条件。
如果我们使用公式t_ ultimate = -TCT_winding x ln[1-(Ic/I_actual)2]来计算,则t_ ultimate = -60秒 x ln [1-(1 /3)2] = 7.06秒,得出TCT_winding(3Ic) = 7.06/5 或 ~1.41秒。
问题2: 由于问题1中的电机无法在3Ic情况下实现耐受30秒,我们可以实现在Ipk为2Ic的情况下耐受20秒吗?
Q2 答: 同样地,使用图 B,我们可以获取2Ic时X对数轴的读数大约为0.057。因此,在 2Ic 时,您的有效TCT_winding(2Ic) = 0.057 x 60 = ~3.42秒,从而可以知道5xTCT = 99.3%的温升时间约为17.1秒,它仍然小于建议的20秒规格。
因此,即使将规格更改为2Ic时耐受20秒,我们也需要选择更大的电机或具有更长TCT_winding的电机,或者再次更改条件规格。
注意: Ic倍数越小TCT_winding对电机整体热时间常数 (TCT_motor)的物理影响越小,当 I_actual/Ic 接近一 (1)时,电机的其他热非均匀材料(例如铝外壳)将发挥主要作用。
结论
显然,在机器设计规划阶段有许多因素需要考虑。针对给定应用的伺服电机和驱动器选择会影响机构在所有条件下成功实现所需性能的机会:正常运行、急停和可预见的潜在事件。如果要求电机的转矩和电流需要有以上一类的要求在较长时间内超过额定连续能力,利用简化的图形方法(图B)可以帮助广泛的风险管理决策克服初始设计的挑战。
本文为读者提供了I_actual/IC过载条件严重性的可视化参考。在I_actual/IC较高的情况下,由于非均匀材料无法在维持TCT_motor主导地位所需的相对时间内传递热量,因此可以相当准确地估计TCT_winding(新)或达到极限温度的时间。
然而,当I_actual/Ic之比接近1时,热力学响应涉及两个指数函数,每个函数都有自己的时间常数(TCT_winding&TCT_motor)。由于非均质材料而导致的热时间常数的这种混合超出了本文的意图,通常需要进一步评估和理解。