自从 20 世纪 30 年代 Hendrik Bode 设计出了一种能够显示频域内增益和相移图的方法,波特图就开始出现在人们的眼前。如今,生成一个显示频域内伺服机构独特指纹的详细频响图,就如同按下电脑按键一样简单。本文讨论了波特图中的五个关键项,及其揭示了机器的哪些信息。
波特图是与伺服机构有关的振幅图和相位响应图的组合,受系统中频率范围的影响。波德图的生成需要大量的高等数学知识,但今天有了强大的微处理器,数字运算可以在几秒钟内完成。振幅 (dB) 和相位(度)的测量值绘制在所测试频率范围的对数刻度上。这些图表显示了机械系统对频率范围的响应情况。振幅和相位会根据机构的设计,按照特定模式发生变化,然后通过该模式,我们可获得系统相关信息。

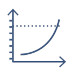
图1:在理想的系统中,振幅图有一条负斜率直线,-20dB/十进位。相位应从 -90° 开始,然后从振幅超过 0 dB 的点开始以负斜率下降。
在非常低的频率下,机械系统根据收到的信号运行,并与频率或振幅保持同相。随着频率增加,机械响应振幅将减少,同时相位开始滞后。我们可以通过使用橡皮筋和挂在其上的几个垫圈来证明这一点。当您慢慢地上下移动橡皮筋时,垫圈将紧跟着移动。当您移动橡皮筋的速度越来越快时,频率就会增加,而由于橡皮筋的柔性,垫圈将无法跟上。在不同的速度下,垫圈会完全停止移动,或失去控制,甚至朝要求的反方向移动。
带宽
带宽与机构的稳定时间直接相关联。带宽越高,达到控制速度或位置的时间就越短。一个机构的带宽与系统的生产力直接相关。在开环波特图中,带宽由振幅图越过 0 dB 的频率决定。

图2:系统带宽是开环图在振幅图中越过 0dB 的点。
稳定性
系统的稳定性与系统在各个运行阶段的表现有关。如果系统运行平稳,且在运动或静止期间从不会出现不稳定情况,则可以认为伺服机构是稳定的。相位和增益裕量是非常好的系统稳定性指标,且可以利用开环图推导出来。裕量越大,系统就越稳定。具体来说,增益裕量是相位首次达到 -180° 时,低于 0 dB(以 dB 为单位)的振幅值。相位裕量就是振幅值越过 0dB 时,相位值与 -180° 的差值。了解系统的稳定性可以确定其在所有条件下是否能够平稳可靠地运行。

图3:表明相对稳定性的相位和增益裕量测量值
并联谐振和共振
任何系统的关键要素都是与整个系统的机械顺应性相关的各种共振频率。系统的每个机械元件都有自己的自然共振频率(波特图),显示出一个反共振和一个共振点——机械元件从系统解耦(反共振节点)或在其共振点(共振节点)被激发。每一对节点都与系统中的一个柔性元件相关。尽管系统可能会有多个共振节点,但第一组节点(最低频率)则是最重要的,因为我们无法实现高于第一个并联谐振节点频率的带宽。共振点为如何通过系统调优来优化系统提供了线索。

图4:将机械装置与波特图所显示的信息关联起来
刚度和负载与电机惯量
波特图显示的另一个有趣的信息就是负载与惯量比。在简单的双体系统中,首个并联谐振节点至首个共振节点之间的宽度(频率差)与惯量比成正比,差异越大,负载与电机惯量比就越大。刚度和负载与电机惯量之间的关系对于了解系统性能至关重要。

并联谐振和共振频率之间相差越大,惯性不匹配就越高
首个并联谐振节点的频率越高,机构的刚度就越高。下述方程式有助于确定首个并联谐振节点:

其中,K 为系统刚度,JM 为电机惯量
系统共振的计算公式为:

其中,K 为系统刚度,JM 为电机惯量,JL 为负载惯量
调优计划
前面几点提供了为优化性能进行系统调优的关键信息。我们可以使用各种滤波技术,包括超前滞后滤波器、陷波滤波器或双二阶滤波器,以改进系统响应。通过使用滤波器组合,我们可以更改振幅和相位值,以改进相位和增益裕量,提高带宽,或消除潜在的共振问题。了解波特图的总体结果有助于做出明智的滤波决定,以实现系统调优。
结论
波特图是一个重要工具,可帮助我们诊断和调整系统,以优化伺服性能。对系统进行调优以达到卓越性能后,就可以将捕获的波特图与基线“黄金图”进行比较,以进行预防性维护或预测性维护。当与“黄金图”进行比较时,耦合或同步带松动就会显示为异常现象,可在损坏发生之前进行纠正。虽然本文只涉及波特图中披露的一些项目,但我们可以使用更先进的波特工具来进一步增强对整个机器结构的认识,并快速指示应该处理的区域。